728x90
반응형
lab-09-1~4
09-2 Weight initialization
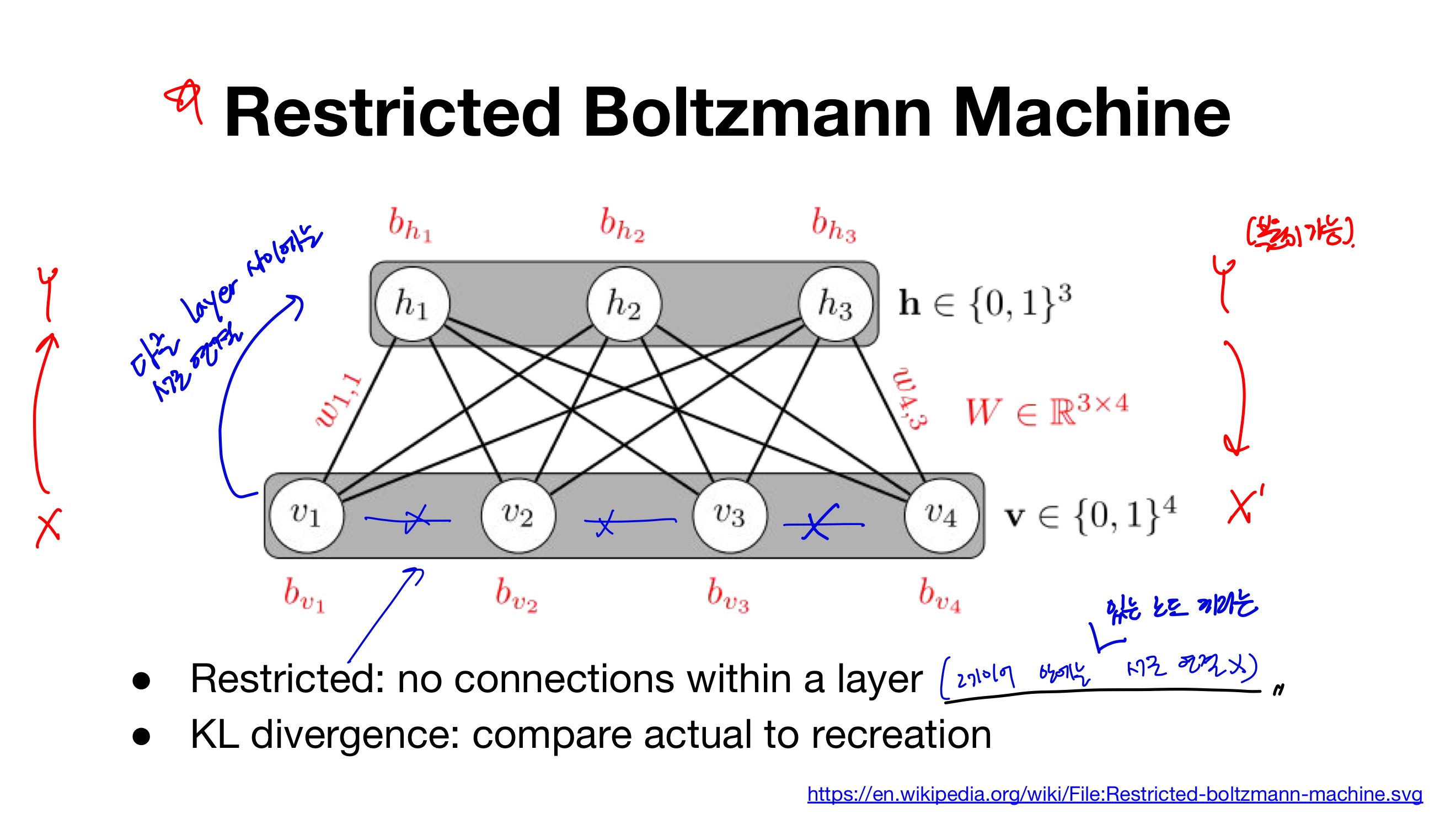
- RBM은 두 개의 층(입력층 1개, 은닉층 1개)으로 구성되어있기 때문에 심층 신경망은 아님
- 다만 RBM은 심층 신뢰 신경망(DBN:Deep Belief Network)을 구성하는 요소로 사용
- X→Y 출력, 반대로 Y-X’로도 복원 가능
- 레이어 안에 있는 노드끼리는 서로 연결 x
- 다른 layer 사이에는 서로 연결 o
- 두 분포가 얼마나 유사한지 측정하는 방법 (forward ↔ backprop을 반복하면서 bias와 weight 조정)

- RBM을 여러번 학습 하는 것: DBM
- pre-training, Fine-training 두 가지 과정으로 나누어진다.
- Pre-training : 두 layer 사이에서 weight를 학습 -> 고정 -> 앞 단의 두 layer 사이에서 다시 weight학습, layer의 개수에 따라 과정을 반복한다.
- Fine-training : 학습된 weight을 가지고 전체 모델에서 학습을 진행한다.

- 실제로 RBM/DBM은 복잡해서 잘 사용하지 않음

- 가중치 초기화로 Xavier, he initialization, + batch nomalization도 사용



09-3 Dropout
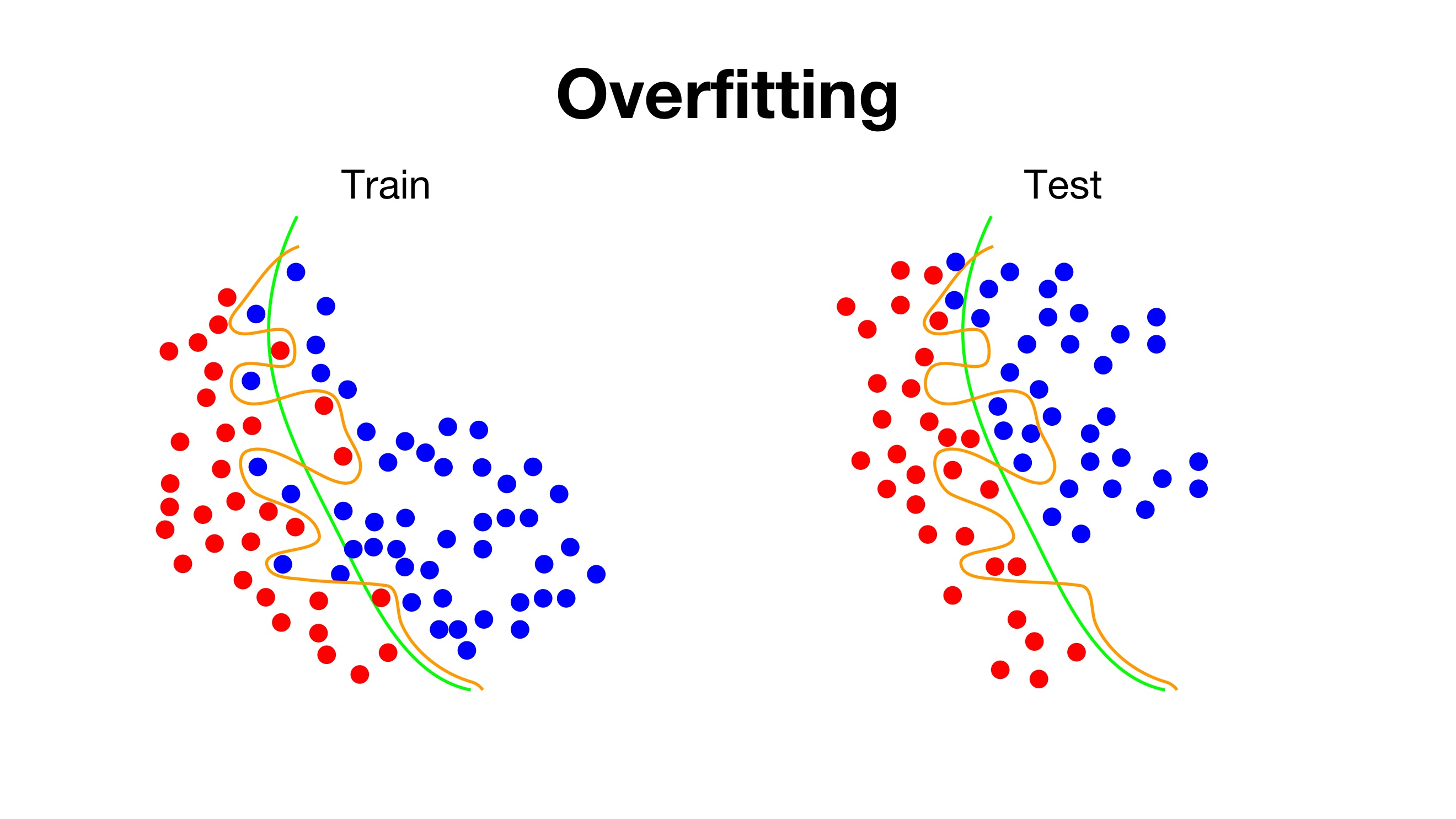
- Underfitting : 주어진 데이터를 충분히 학습하지 못하여 낮은 성능을 보인다.
- Overfitting : 주어진 데이터를 과도하게 학습하여 높은 성능을 보인다. 그러나 unseen data에 대해서는 좋은 성능을 보이지 못한다.

- 오버피팅 방지
- 더 많은 트레인 데이터
- 피처 수 줄이기
- 정규화
- dropout
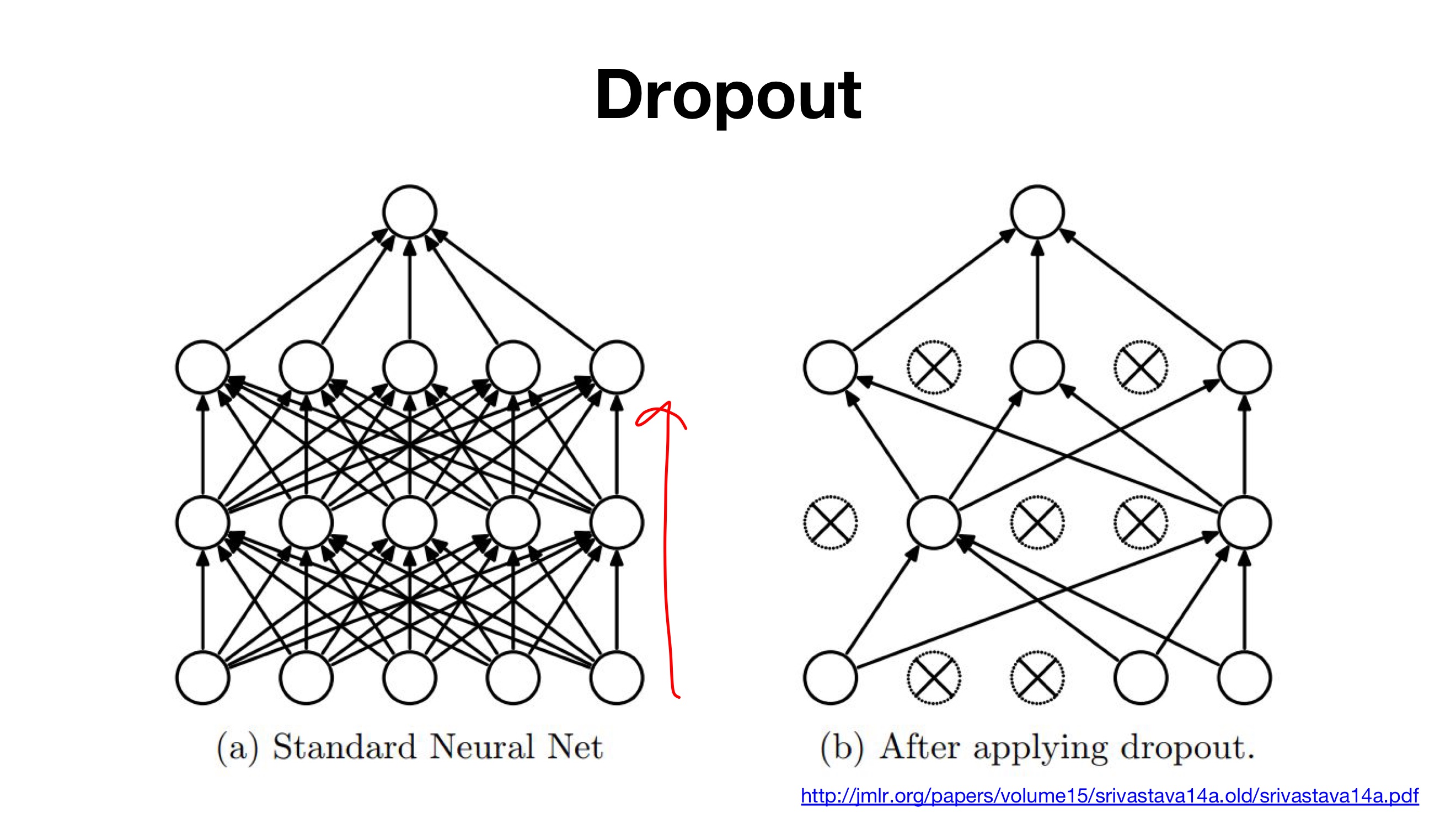
> 학습을 진행시, drop out probability에 맞춰 노드(정점, 꼭지점)들을 비활성화 해준다. > 비활성화되는 node들은 임의(random)로 정해진다. > Drop out은 overfitting을 방지하고, 매번 랜덤하게 node들이 선택되기에 매번 다른 형태의 모델로 학습하는 효과를 가진다.(즉, network ensemble 효과)


09-4 Batch Normalization
- gradient vanishing( gradiant가 작아져서 소멸하는)
- ↔ exploding 그 반대( gradiant가 너무 커지게 되는 경우)


- 기울기 소실 문제 해결
- 활성화 함수 바꾸기( eX) sigmoid → ReLU)
- 가중치 초기화
- 작은 학습률
- 배치 정규
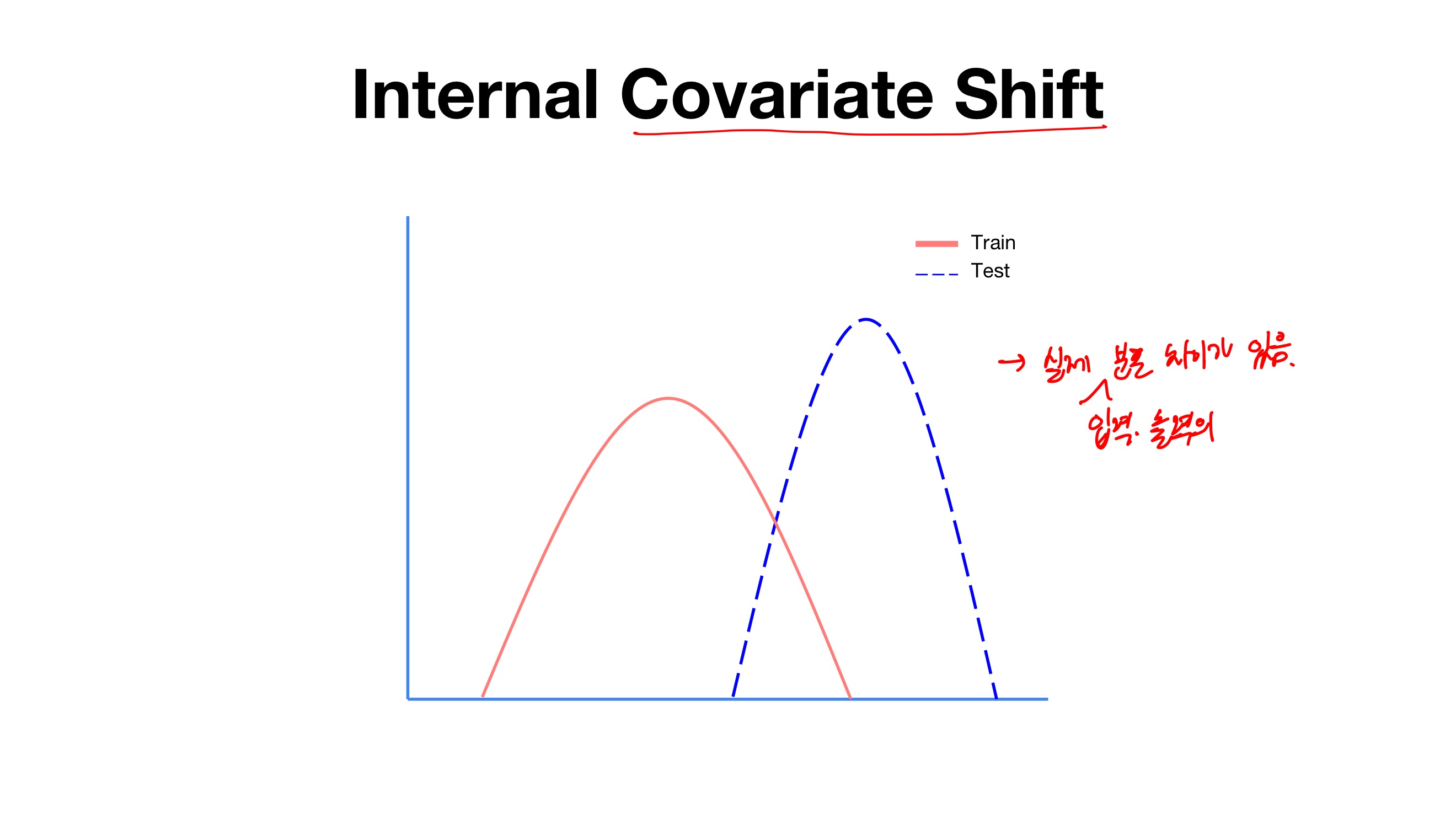
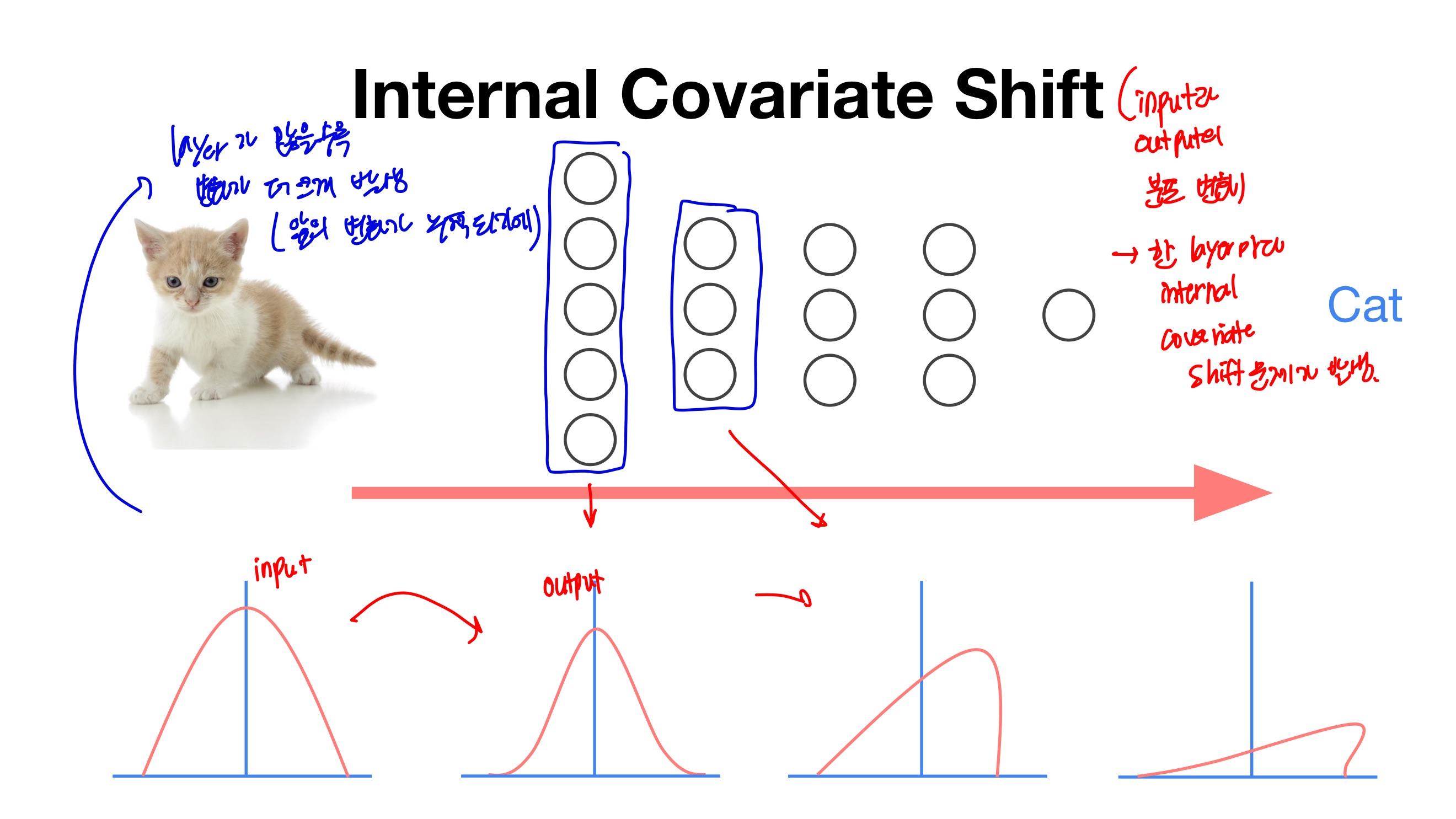
- Layer가 더 깊어질수록 고양이 이미지 분포가 왜곡 되는 현상을 보이고 있다.
- 고양이 이미지 분포가 왜곡이 되면 이미지를 고양이로 인식하지 않는다.
- layer가 많을수록 변화가 더 크게 발생 (앞의 변화가 누적되기에)
- 가중치가 조금만 달라지면 완전히 다른 값을 얻을 수 있다는 점.
- 를 해결하기 위해, 각 layer에 배치 정규화 과정을 추가해준다면, 가중치의 차이를 완화하여 보다 안정적인 학습이 이루어질 수 있다.

- 먼저, hidden layer의 활성화함수 입력값or출력값 상태인 배치의 평균과 분산을 계산한다.
- 이후, 해당 배치를 평균 0, 분산 1이 되도록 정규화한다.
- 엡실론은 분모가 0 이 되는 것을 막기 위한 아주 작은 숫자(1e-5)이다.
- 정규화 이후, 배치 데이터들을 scale(감마(γ)), shift(베타(β)) 를 통해 새로운 값으로 바꾼다.
- 데이터를 계속 정규화 하게 되면, 활성화 함수의 비선형 성질을 잃게 되는 문제가 발생한다.
- 예를 들면, 아래 그림과 같이 Sigmoid 함수가 있을 때, 입력 값이 N(0, 1) 이라면, 95% 의 입력 값은 Sigmoid 함수 그래프의 중간 (x = (-1.96, 1.96) 구간)에 속하게 된다.

- 해당 부분이 선형이기 때문에, 비선형 성질을 잃게 되는 것이다.
- 하지만, 감마(γ), 베타(β)를 통해 활성함수로 들어가는 값의 범위를 바꿔줌으로써, 비선형 성질을 보존하게 된다.
- 감마(γ), 베타(β) 값은 학습 가능한 변수이며, Backpropagation을 통해서 학습이 된다.
- Layer가 깊어질수록 분포가 왜곡 되는 현상을 막기 위해서 각 layer들마다 Normalization을 하여 변형된 분포가 나오지 않도록 한다.
- Normalization을 하면 activation function의 Non - linearity 성질을 잃게 되는 경우가 발생한다.
- 이를 보완하기 위해서 Normalization값에 gamma를 곱하고 beta를 더한 뒤 back-prop 과정에서 gamma와 beta를 학습시켜준다.

테스트 단계
- 테스트 단계나 추론 단계에서는 평균과 분산을 계산할 미니배치가 없기 때문에, 전체 Training Set의 평균과 분산을 사용한다.
- 하지만, 엄청나게 많은 전체 Training set에 대한 평균과 분산을 계산하는 것은 무리이기 때문에,
- 아래의 식과 같이 모델 학습 단계에서 사용한, 각 n개의 미니배치에 대한 평균과 분산을 이용해, 전체 Training Set의 평균과 분산을 대신할 수 있다.
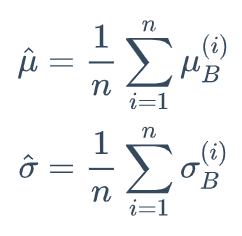
- 하지만, 위와 같은 방법 대신, 미리 저장해둔 n개의 미니 배치의 이동 평균을 사용하여 해결한다.

- 이러한 이동 평균과 분산을 위해, 모델 학습 단계에서 매 미니배치마다 이동 평균과 분산을 저장해놔야한다.
- 그래야 테스트 시, 모델 학습 단계에서 저장한 이동 평균과 분산을 사용할 수 있다.
- 위의 식에서 α값은 일반적으로 1에 가까운 0.9, 0.99, 0.999로 설정한다.


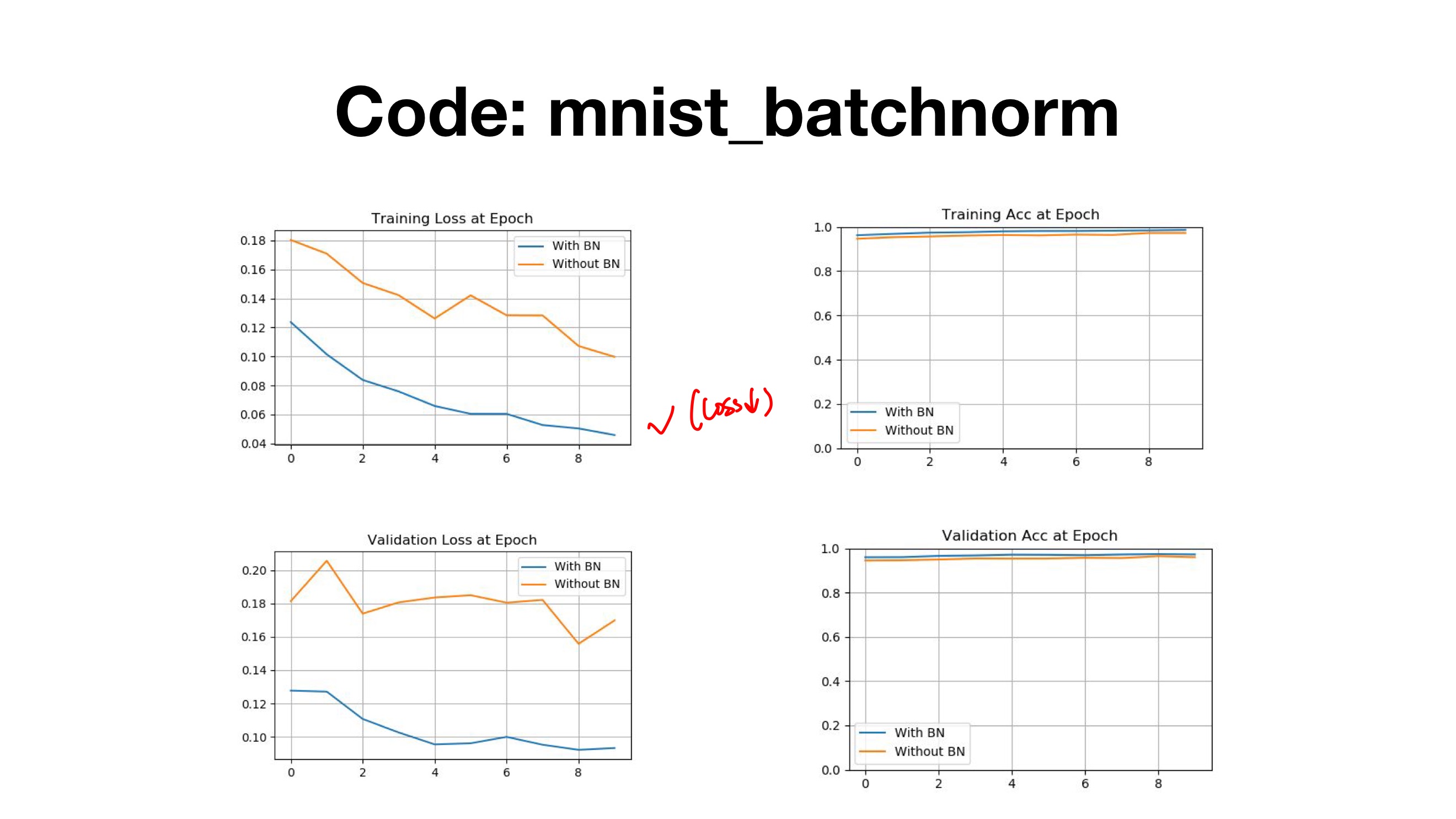
728x90
반응형
'Deep Learning > 2023 DL 기초 이론 공부' 카테고리의 다른 글
| [모두를 위한 딥러닝 시즌 2] lab-10-1~2 (0) | 2023.07.09 |
|---|---|
| [모두를 위한 딥러닝 시즌 2] lab-01-1~08-2 (0) | 2023.07.09 |
| [밑바닥부터 시작하는 딥러닝 2] chap1(신경망 복습) (0) | 2023.07.09 |
| [밑바닥부터 시작하는 딥러닝 2] chap2(자연어) (0) | 2023.07.09 |
| [밑바닥부터 시작하는 딥러닝 2] chap3(word2vec) (0) | 2023.07.09 |













