날짜: 2023년 7월 2일
Part 1. Matrix Decomposition(행렬 분해)
1. Determinant(행렬식)
- 3x3 matrix의 Determinant를 2x2 matrix의 Determinant로 다시 정의할 수 있음 → Laplace expansion이라고 칭함

- Determinant의 성질

2. Trace
- Determinant와 유사한 의미
- Matrix의 어떤 Diagonal Entry를 다 더한 형태를 Trace라고 함
- 덧셈 분해가 가능함

3. Eigenvalue and Eigenvector
- Ax = lambdax 로 표현될 때, lambda의 scala value인 lambda와 이런 x Vector를 Eigenvalue와 Eigenvector라고 부르게 됨
- Eigenvector들이 unique 하지는 않는다는 특징을 지님

1. Determinant A는 Eigenvalue들의 곱셈으로 표현이 됨
2. Trace는 Eigenvalue들의 덧셈으로 표현이 됨

4. Cholesky Decomposition

5.Diagnonal Matrix
- Diagonal Entry만 존재하고, 나머지 Entry는 다 0인 형태를 Diagonal Matrix라고 함
- 다양한 연산들이 매우 쉽게 되는 장점을 지님

- 간단한 형태로 만들 수 있음

6. Singular Value Decomposition
- 어떤 Matrix A가 주어졌을 때, UsigmaV로 분해하는 꼴을 Singular Value Decomposition이라고 함
- 항상 존재 → 더 유용하게 쓰임

Part 2. Convex Optimization
1. Unconstrained Optimization and Gradient Algorithms
- 내적해서 0이 되는 방향 중에 반대방향으로 d를 선택하는 것을 Steepest Gradient Descent라고 부름 = Gradient Descent
2. Batch gradient
- 모든 data point를 다 고려해서 계산하는 업데이트를 batch gradient라고 부름
3. Mini-batch gradient
- Data point가 n개 있을 때, 어떤 특정 subset을 구해서 그 subset에 있는 Gradient만 계산해서 업데이트
4. Stochastic Gradient Descent(SGD)
- mini-batch gradient의 어떤 gradient가 어떤 original batch gradient를 잘 근사할 수 있게 이런식으로 디자인해서 업데이트하는 방식을 stochastic gradient라고 함
⇒ 데이터가 너무 많을 때 활용
5. Adaptivity for Better Convergence: Momentum
- 이전에 업데이트 했던 방향을 추가적으로 더해줌 (관성의 법칙)

6. Convex Optimization
- Set이 있을 때, point를 두개를 잡고 x1과 x2를 가르는 선분을 그음. 이 선분이 항상 Set 안에 있을 때를 convex set이라고 칭함

⇒ 첫번째 도형만 convex set
- f라는 함수를 최소화하고, f에 대한 조건을 다루는 어떤 f가 어떤 x라는 어떤 Set 안에 속해 있다고 가정을 하면, f가 convex 함수이고, 이런 subset을 이루는 x가 convex set이 될 때, convex optimization이라고 얘기함

- Examples of Convex or Concave Functions

Part 3. PCA
1. PCA
ex) 집을 살 때 고려해야하는 5가지 경우가 있다고 가정
- 5가지를 고려하는 것보다, size에 대한 요소 하나, location에 대한 요소 하나, 즉 2가지로 줄여준다는 방법론이 있다고 가정했을 때, 더 수월하게 집을 살지 말지를 결정할 수 있게 됨 ⇒ 이 과정이 바로 PCA라고 할 수 있음
2. PCA Algorithm
1. Centering: 각 데이터에 대한 평균을 구하고 (x1,x2,x3) 각 차원마다 평균을 구해 그 평균을 빼줌 ( 원점을 중심으로 정렬하는 과정 )
2. Standardization: 분산을 구하고, 분산으로 normalization해주는 과정
→ 각 차원을 평균이 0이고, 분산이 1이 될 수 있도록 만드는 선형 변환의 과정
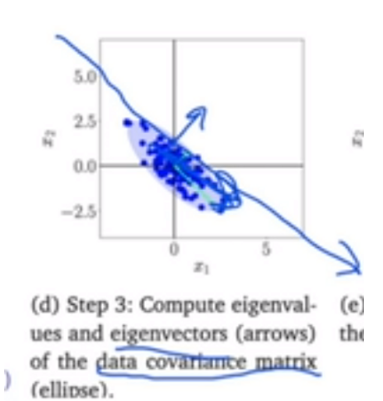
3. Digenvalue/vector: M개(축소하고 싶은 차원의 개수 ex) 5→ 2, M= 2)의 Eigenvector을 구함
4. Projection: Data point를 축소시키는 과정
5. Undo stadardization and centering: 1,2번의 과정을 다시 원래의 분포로 옮겨주는 역할
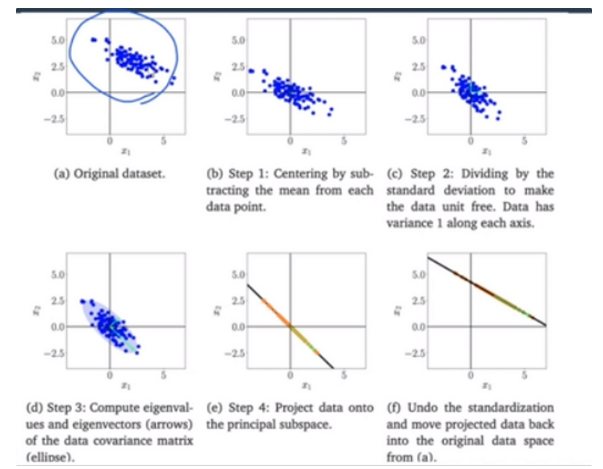
1. 원점으로 이동하는 것을 볼 수 있음
2. 나눠주면 분산이 1이 되는 효과가 됨
3. step2의 데이터를 데이터라고 가정하고, 이 데이터의 data covariance Matrix를 구하게 됨 ⇒ Eigenvector을 구하게 되면 대각선 방향의 eigenvector이 더 크기 때문에 대각선 방향으로 projection 시킴
※ 이 평면으로 가장 가까운 point를 찾아서 데이터를 squeezing 함 (step 4)
4. 마지막은 첫번째 과정으로 거꾸로 다시 계산하는 과정
⇒ 원래는 2차원 데이터였는데, 선분 위에 있는 1차원 데이터가 됨.
3. Idea

- 분산이 큰 방향은 데이터가 가장 많이 퍼져있는 방향이므로, 해당 축으로 데이터를 투영하면 최대한 많은 정보를 유지할 수 있음.
- 분산이 작은 방향은 데이터의 변동성이 작기 때문에 해당 축으로 투영하면 데이터의 정보 손실이 크게 일어날 수 있음
4. 수식

'대외활동 > 2023 LG Aimers 3기' 카테고리의 다른 글
| Module 7. 딥러닝 (Deep Learning) (KAIST 주재걸 교수) (0) | 2023.07.15 |
|---|---|
| Module 6. 강화학습 (Reinforcement Learning) (고려대학교 이병준 교수) (0) | 2023.07.15 |
| Module 5. 지도학습 (분류/회귀) (이화여자대학교 강제원 교수) (0) | 2023.07.08 |
| Module 4. Bayesian (고려대학교 김재환) (0) | 2023.07.04 |
| Module 3. SCM & 수요예측 (고려대학교 이현석 교수) (0) | 2023.07.04 |



