[Standford_cs231n] Lecture 3 ) Loss Functions and Optimization

 

1. Loss Function

• 사진에서 보이는 score가 낮을수록 W의 영향력도 안좋은 것이라고 말할 수 있음( 분류를 잘 하지 못했으므로 )

• W가 좋다 안좋다 정도로 정량화 할 수 있는 것이 필요함 ⇒ loss function

• W(가중치)가 얼만큼 좋고 안좋다로 나타낼 수 있는 함수가 바로 손실함수임.

1. SVM loss( hinge loss )

2. softmax loss( cross entropy )

1-1) Multiclass SVM loss

• 정답클래스≥정답아닌클래스+1 ⇒ loss=0 ( 매우 좋음 )

ex)

1. cat과 car의 경우 : 정답클래스(3.2)≥정답아닌클래스(5.1)+1 이 아니므로 해당 값을 loss 값으로

2. cat과 frog의 경우 : 정답클래스(3.2)≥ 정답아닌클래스(-1.7)+1 이므로 loss 값은 0

3. car frog class도 다 해줌

• 다 더해준 후 평균값 ⇒ 최종 loss

---

추가 SVM loss 특징

• 1. 데이터에 민감하지 않음

  

  • score 값을 바꾼다 해도 loss는 똑같이 0임

  • cat에 +1 하던지 frog에 +1 하던지 자동차 값이 더 높기 때문임.⇒ 정답 클래스가 다른 클래스보다 높냐 에만 관심을 가짐.

• 2. 최소, 최댓값 (최소: 0 값, 최댓값: 무한대)

  

• 3. W가 작아져서 score가 0에 근사해지면 class-1값이 나옴.

  

  

  ex)

  클래스가 3인 경우: 2+2+2/3 ⇒ 2

  클래스가 10인 경우: 9+9+9+,,,,,,/10 ⇒ 9

  ⇒ sanity check라고도 부름.

• 4. 정답 클래스 값 제외시키면 loss+1값이 되어버림

  ⇒ 그럴경우 loss가 1일 때가 가장 좋은 값이 되어버리는데 0이 가장 좋다 라고 표현하는게 더 편하기 때문에 정답 클래스는 제외시킴.

  

  

• 5. sum 대신 평균 사용할 경우: 값의 변화는 없음(평균하기에 scale만 작아짐)

  

• 6. 제곱승 할 경우: 값이 달라짐( 극과 극으로 표현하기에 좋음)

  ⇒ 매우 좋고 매우 안좋다로 표현 가능하지만 잘 안쓴다.

  ⇒ 비선형됨 ⇒ squared hinge loss라고 부름

  

• 7. 이 친구의 문제점

  ⇒ W가 여러개가 될 수 있음.

  

  ⇒ score에 2,3배를 해도 값이 같게 나와버림

  즉, W가 여러개가 나온다는 것 ⇒ unique한 W가 없다는 것을 의미하기도 함.

  그래서 나온 것이 규제임.

1-2) Regularization

• loss값이 줄어든다고 해서 좋은 model이라고는 할 수 없음 ⇒ 오버피팅 문제가 발생.

• 뿐만 아니라 위의 svm loss의 문제점인 W값이 여러개가 된다는 점에서 규제화가 나옴

ex) train에게만 맞는 것을 학습시키려고 할 때 이 정도의 패널티는 감안해야돼~ ⇒ 규제화의 기본 뜻.

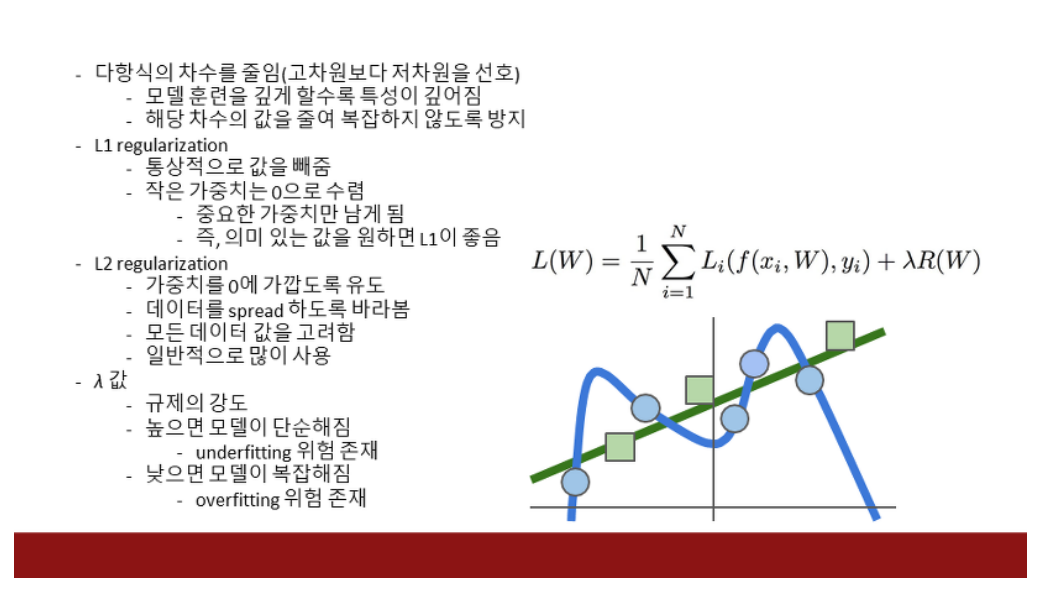
• L1 regularization(Lasso)기존 cost function 뒤에 L1항 추가.
  • weight 값이 0으로 수렴하는 것이 많은 형태. 이를 Sparse matrix(희소 행렬)라고 함
  • 위에서 0의 값이 많다는 이야기는 어떤 특징들은 무시하겠다는 이야기로 볼 수 있음.
• 

• L2 regularization(Ridge)

  

  • weight의 값이 큰 값은 점점 줄이며 대부분의 값들이 0의 가까운 값을 가지는 가우시안 분포를 가짐.
  • weight이 0이 아니라는 점에서 모든 특징들을 무시하지 않고 조금씩은 참고 하겠다라고 볼 수 있음.

  

  • 이럴 경우, L1은 w1을 선호함 → 0 이 많기 때문
  • w2는 L2가 선호함 → 전체적으로 0에 가깝게 퍼져있기에.
  
  ⇒ 만약 (1,0) vector가 있을 때, L1으로 계산하면 |1|+|0|=1이 되고 L2로 계산하여도 1+0=1이 됨.⇒ 값이 균등하게 작을 때에는 L2의 값이 더 작아지게 됨. 따라서 Error에 더 작은 penalty를 주게 됨즉, L1의 경우, 값이 작아진다 한들
  • L1, L2 연산한 값을 Error에 더하므로 연산 결과가 작아지는 값을 선호합니다. 이 값이 너무 커져 버리면 오히려 학습하는 데 방해가 될 수 있기 때문입니다. 따라서 L1 보다 L2를 많이 사용하는 이유이기도 함.
  ?????
•  
•  
• ⇒ 반면 (0.5,0.5) vector가 있을 때, L1으로 계산하면 |0.5|+|0.5|=1이 되지만 L2로 계산하면 0.52+0.52=0.25+0.25=0.5가 됨. 
• 의문점: 왜 L1은 피처 설렉션 느낌이 되고, L2는 균등한 피처에 유용한지?

1-3) Softmax Classifier(cross entropy)

• 원하는 클래스의 점수를 exp 취해서 나눠줌

• 이후, -log를 취한 후 loss를 구함⇒ exp를 취하고, -log를 취하는 이유는 무엇일까?
  1. softmax는 multinomial logistic regression(시그모이드- 로지스틱)⇒ 따라서 exp를 사용
  2. -log 취하는 이유는 -를 곱하게 되면 확률(y)값이 1이 될수록 log1 ⇒ 0에 가까워짐 ⇒ 따라서 -log를 취해 loss값을 구해줌.
• 

 

1-4) svm loss와 softmax classifier의 차이

• 둔감 vs 민감 차이

• hinge loss의 경우 그냥 정답 클래스가 정답 아닌 클래스 +1 보다 크면 끝임

• softmax의 경우, 확률로 계산되기 때문에, 데이터가 조금만 바껴도 확률이 막 바껴버림 ⇒ 개민감.

2. Optimization

• w가 좋은지 안좋은지에 관한 loss 함수를 구했음 ⇒ 어떻게 해야 좋은 weight를 찾아갈 수 있는가에 대한 답이 바로 최적화 파트.

• 산속에서 골짜기를 내려가는 것과 같음

• loss가 0인 지점을 찾아가는 것.

2-1) Random search 임의 탐색

1. 그냥 랜덤하게 포인트를 찾는 것.

2. 임의의 점인 w값을 랜덤하게 찍고 거기서 최적화 방법을 통해 w를 구함

3. 성능 천차만별

2-2) local geometry 경사 하강법

1. 수치적 방법

2. 해석적 방

• h를 0에 가깝게 이동

• loss 감소 1.25347 → 1.25322

• 경사값(기울기): -2.5

이러한 방식으로 모든 W에 대해서 이를 반복하면 모든 gradient dW 값을 구할 수 있음.

이 방식을 Numerical gradient라고 한다.

⇒ 개느림

• 그래서 나온 방식이 해석적 방법

• W가 변할 때 loss를 알고 싶은 것뿐임. ⇒ 경사하강법

2-3) Stochastic Gradient Descent

• 기존 Gradient Descent를 구하기 위해서는 loss function이 필요함

• 이 때 전체 트레이닝 셋의 loss 평균을 구했음

• ⇒ 시간 개오래 걸림

• 그래서 사용하는 것이 SGD ⇒ 미니배치단위로 나눈 트레이닝 샘플을 나눠서 사용하는 방식

3. 특징변환(피처 특징 추출과 같은 말)

• 사실 Linear Classification은 이미지에서는 그리 좋은 방법이 아님

• 그래서 DNN이 유행하기 전에는 Linear Classifier를 이용하기 위해서는 두가지 스테이지를 거쳐서 사용

1. 이미지의 여러가지 특징표현을 계산
   • 모양새, 컬러 히스토그램, edge 형태와 같은 특징표현을 연결한 특징벡터

2. 이 특징벡터를 Linear Classifier에 입력값으로 사용

3-1) 컬러 히스토그램

• 이미지에 관한 각 픽셀을 다 추출해서 해당하는 색에 픽셀값을 넣는 개념 ( 이 픽셀은 무슨 색인가에 대한 갯수 세기)

• 개구리의 경우 초록색이 많음

• 이거에 대한 특징을 피처로 뽑아 input으로 사용.

3-2) Histogram of Oriented Gradient

• 방향값을 히스토그램으로 표현하는 것.

• 8*8 픽셀로 구성된 구역을 9가지의 엣지 구역으로 나눠서 각 9가지의 bin에 몇개가 속하는지를 피처로 추출해낸 것

• 이미지를 8*8로 잘라서 해당 값에 어떤 각도가 많은지를 히스토그램으로 나타내서 특징 추출.

• 마찬가지로 피처로 뽑아서 input에 사용

3-3) Bag of words

• 이미지를 막 자름

• 이거를 클러스터같은 것으로 군집화 함

• 그러면 각도나 색깔 등의 특징이 나올 것임.

• 이후, 새로운 이미지가 들어오면 이미지를 잘라서 기존에 만든 클러스터랑 비교해 어떤 특징이 있는지 비교

---

• 이 방법은 NLP에서 영감을 받은 방식으로, 어떤 문장에서 여러 단어들의 발생빈도를 세서 특징벡터로 사용하는 방식을 이미지에 적용한 것입니다.

• 우리는 이미지들을 임의대로 조각내고, 각 조각을 K-means와 같은 알고리즘으로 군집화 합니다.

• 다양하게 구성된 각 군집들은 다양한 색과 다양한 방향에 대한 edge도 포착할 수 있습니다.

• 이러한 것들을 시각 단어(visual words) 라고 부릅니다.