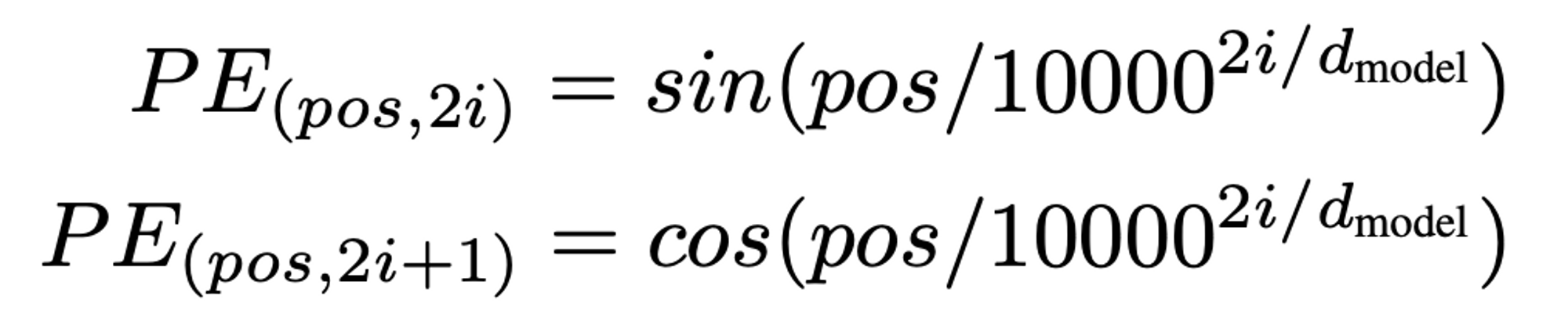Transformer

 

 

 

1. overall architecture

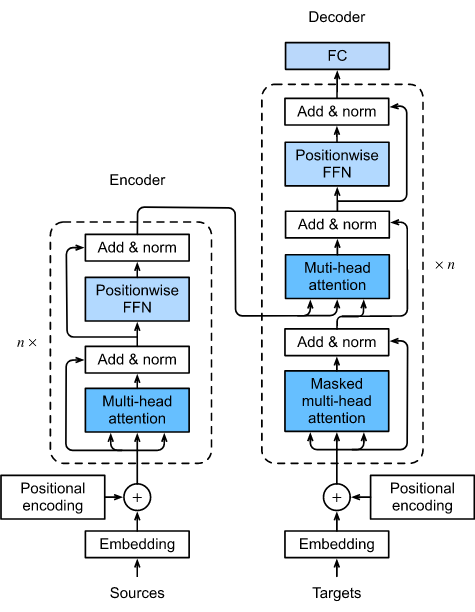
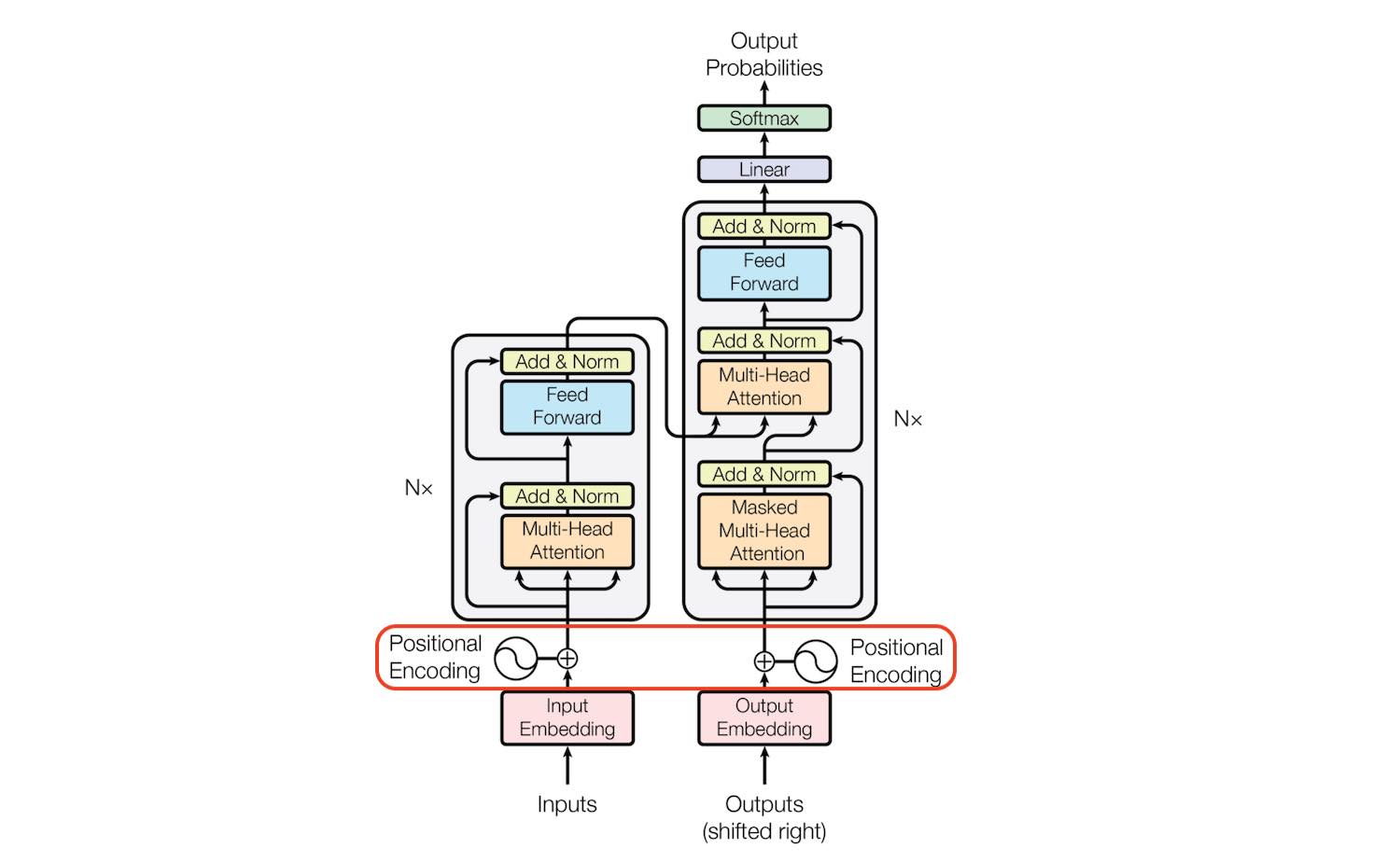
2. overall procedure

• encoder의 경우
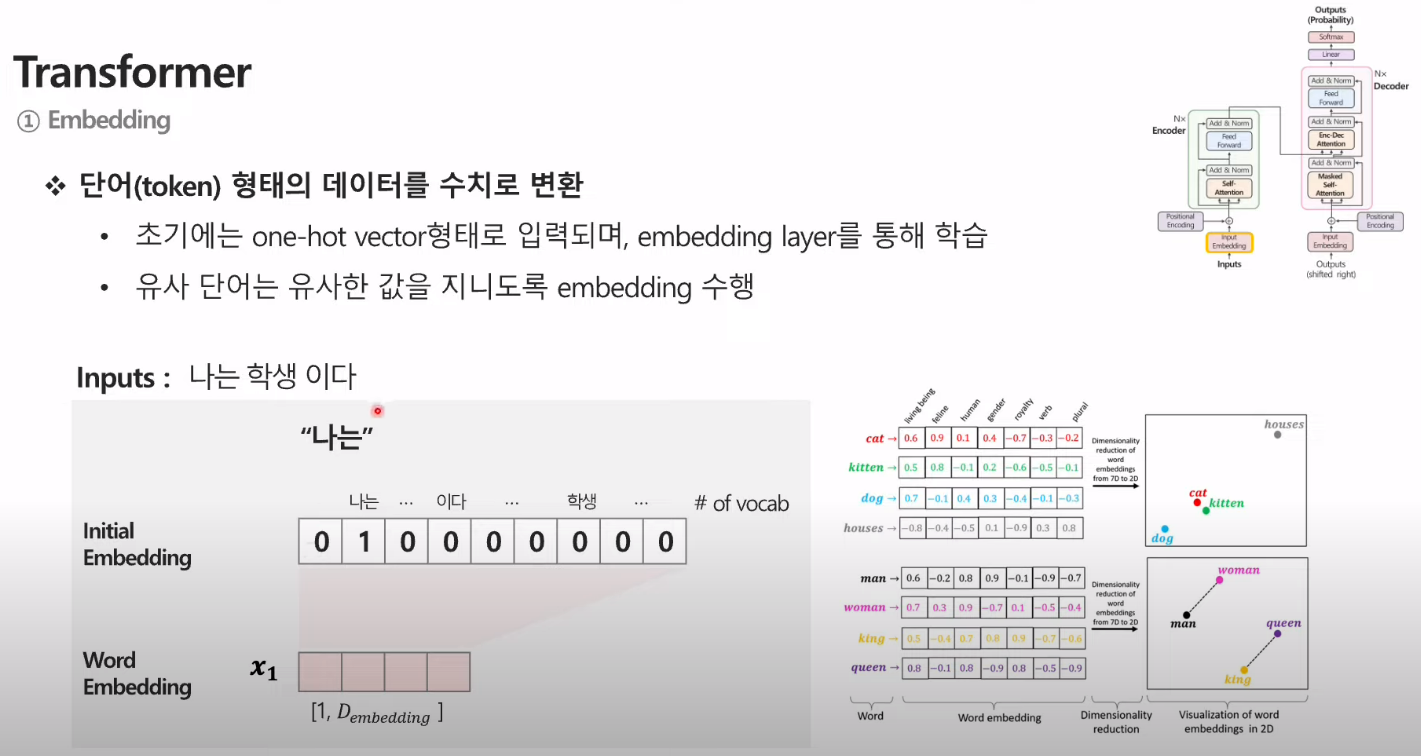
  1. input 문장을 넣고 embedding 벡터로 바꿔줌
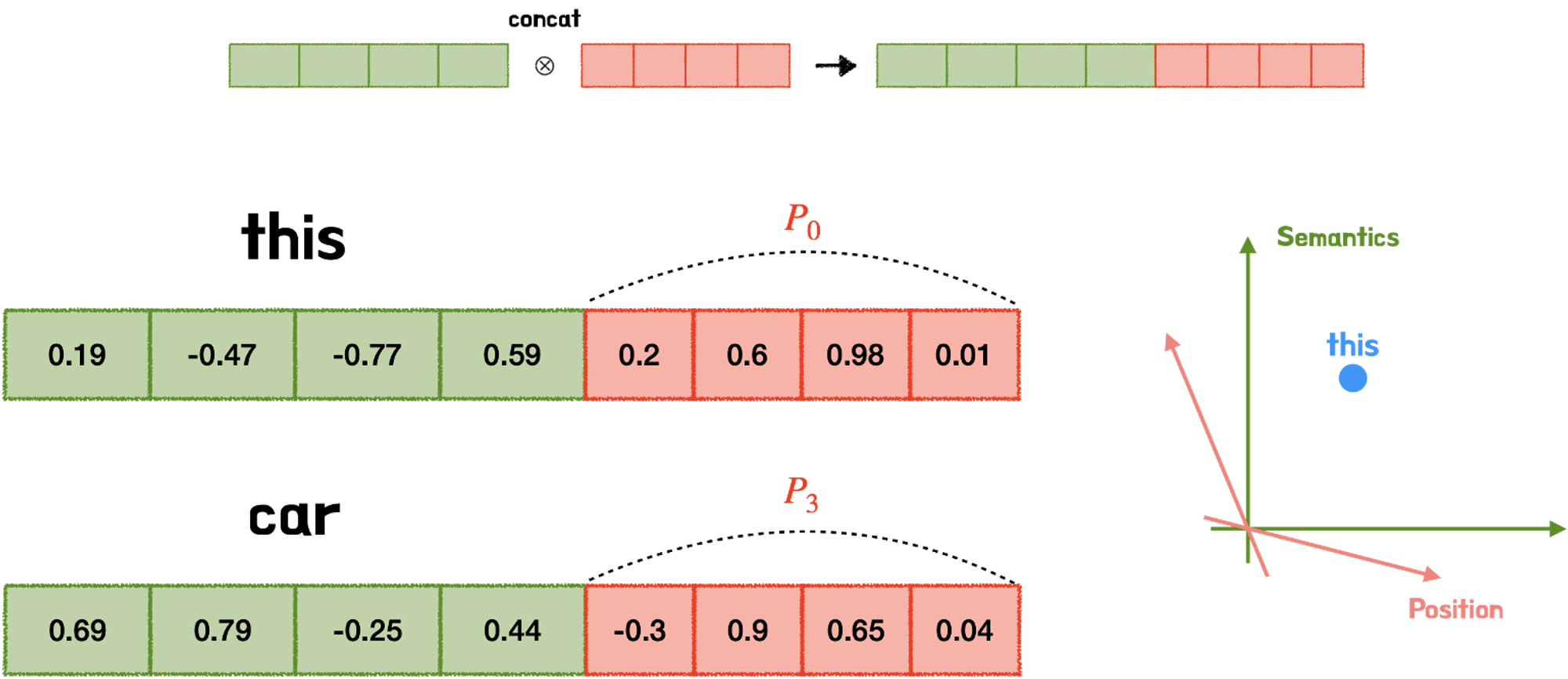
  2. positional encoding을 더해주어 각 단어의 순서에 대한 정보를 부여함.
  3. 더해서 multi-head attention을 수행
  4. 이 때, 같은 embedding의 값을 Q,K,V로 분배. (Q,K,V)는 서로 같은 값.
  5. ex) head가 3개면, 각 Q,K,V에 해당하는 가중치 3개씩 존재함 (Linear) ⇒ 총 9개의 다른 값이 생기게 됨
  6. 이때, V는 encoding의 embedding에서 나온 값에 가중치 곱한 것을 의미.
  7. 하나의 head당 Q와 K를 곱해서 softmax 함수를 거친 후, V값과 곱함
  8. 이 각각 곱한 3개의 head 값들을 concat하고 linear를 통해 값을 냄.
  9. 7번에 대한 값과 2번에 대한 값을 더한 후 정규화 함.
  10. 이후 순전파하고 또 8번 값과 순전파한 값을 더하고 정규화
  11. 반복

  ---

• decoder의 경우
  1. 학습 시) 정답 문장을 embedding으로 넣음. positional encoding을 더해서 각 단어의 순서에 대한 정보 부여.
  2. 더하고, encoder와 같이 각 Q,K,V 생성.
  3. 똑같이 Q와 K를 곱함
  4. mask를 거치게 되는데, 얘는 decoder embedding으로 받은 뒷부분의 단어들은 0으로 만들어줌.
  5. 그 단어만 뽑은 값과 그 앞의 단어들만 softmax를 통해 확률로 변환하고, V값과 곱해줌
  6. 각각 나온 3개의 head 값들을 concat하고 linear을 통해 값 추출
  7. 6번의 값과 1번의 값을 더하고 정규화
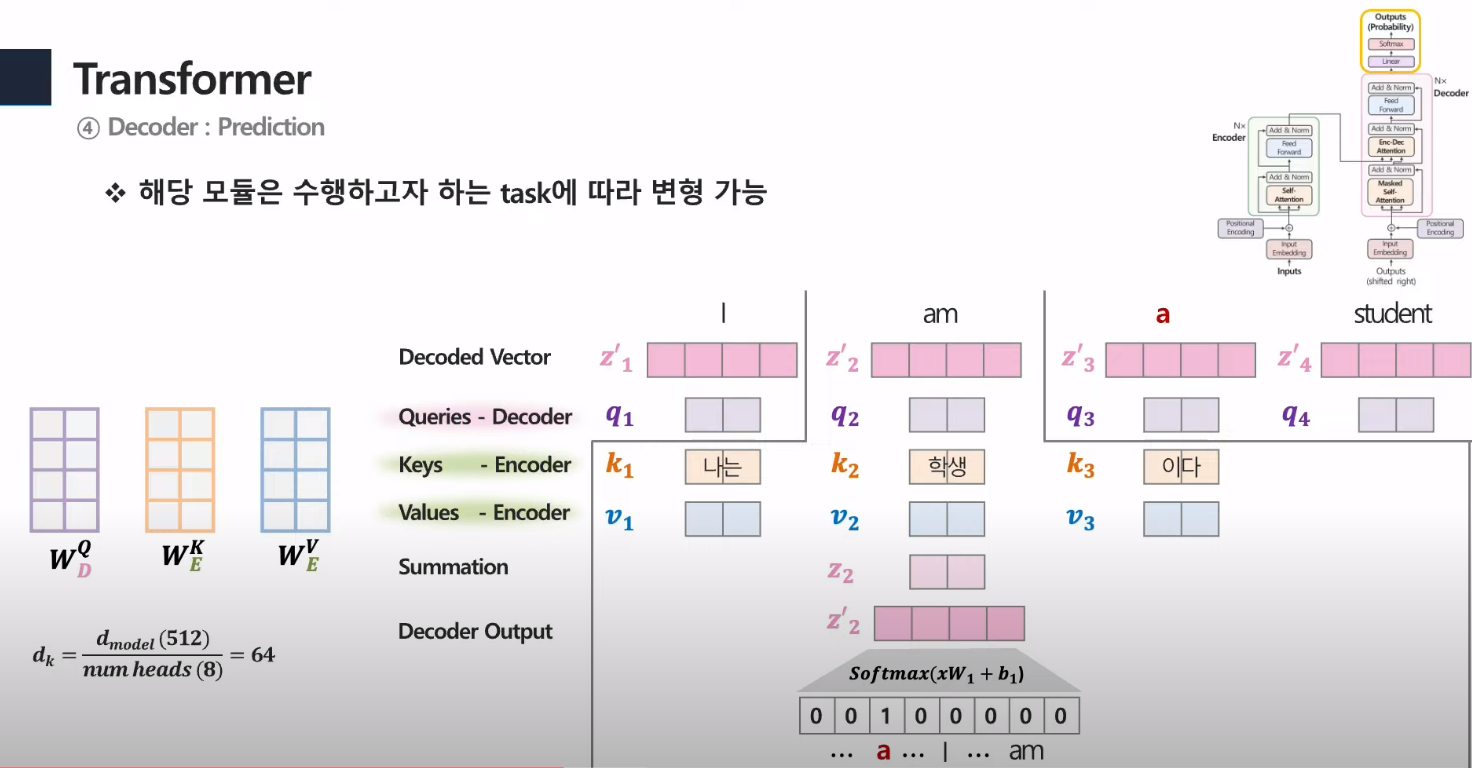
  8. 두번째 multi head attention의 경우, Q는 7번의 값을 통해 만들고, K와 V는 encoder의 마지막에서 나온 값을 사용함.
  9. 이후, 똑같이 K와 Q 곱하고 softmax 통해 확률 구해서 V값과 곱함.
  10. 똑같이 더하고 정규화
  13. FC layer갔다가 또 FC 전의 값과 이후 값을 더해주고 정규화.
  14. 그 나온 아웃풋 값을 다시 첫번째 masked 계층으로 ㄱㄱ
  15. 첫번째 아웃풋과 decoder embedding 값을 활용해 반복.

---

1. Embedding

• input 문장으로 들어온 애들을 원핫벡터로 바꿔줌

• 이후 적절한 크기로 word embedding 진행 (유사한 단어끼리는 유사한 값으로)

2. Positional Encoding

• 순서 정보를 갖도록 하는 벡터.

• word embedding 계층과 같은 크기의 벡터를 생성한 후 더해줌.

3-1. Encoder: Self-Attention(Multi-Attention)

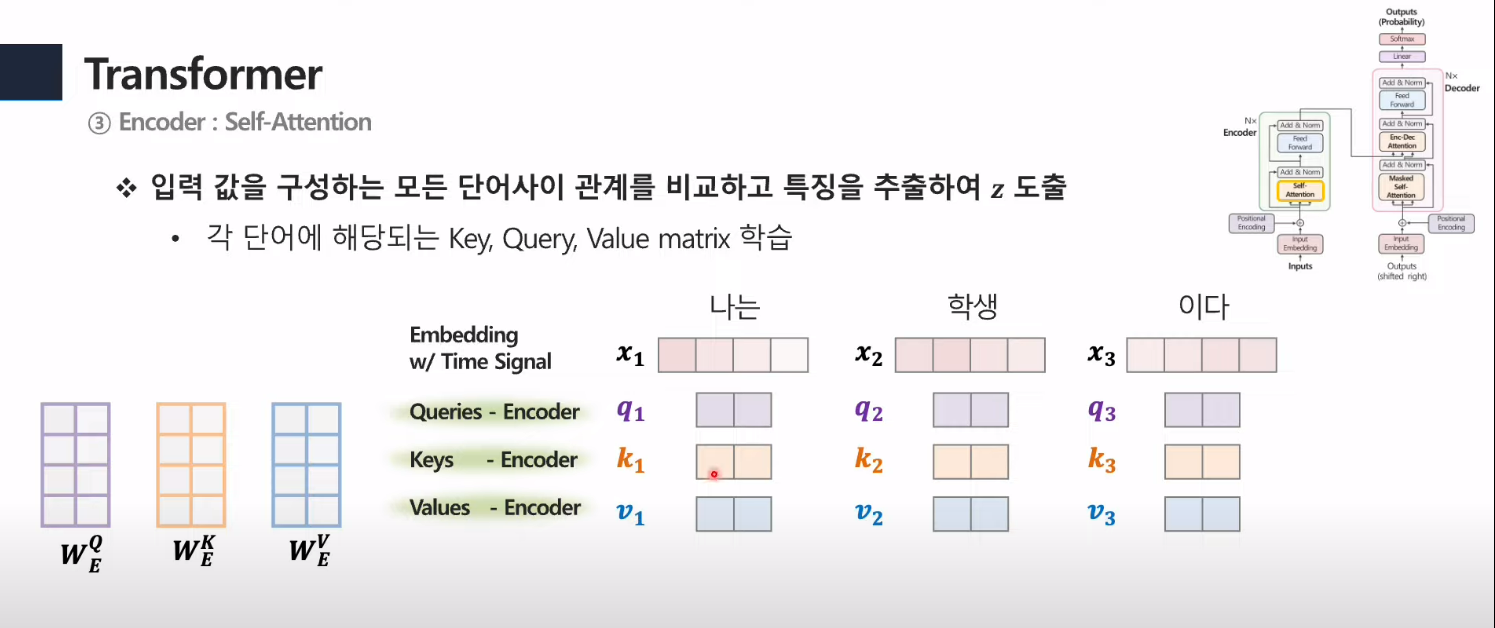
• postional encoding을 더해준 각 단어의 벡터(1x4)와 각각의 Q,K,V의 가중치(4x2라고 가정)를 곱함. ⇒ 각각의 다 다른 Q,K,V가 만들어질 것임 (1x2) 크기

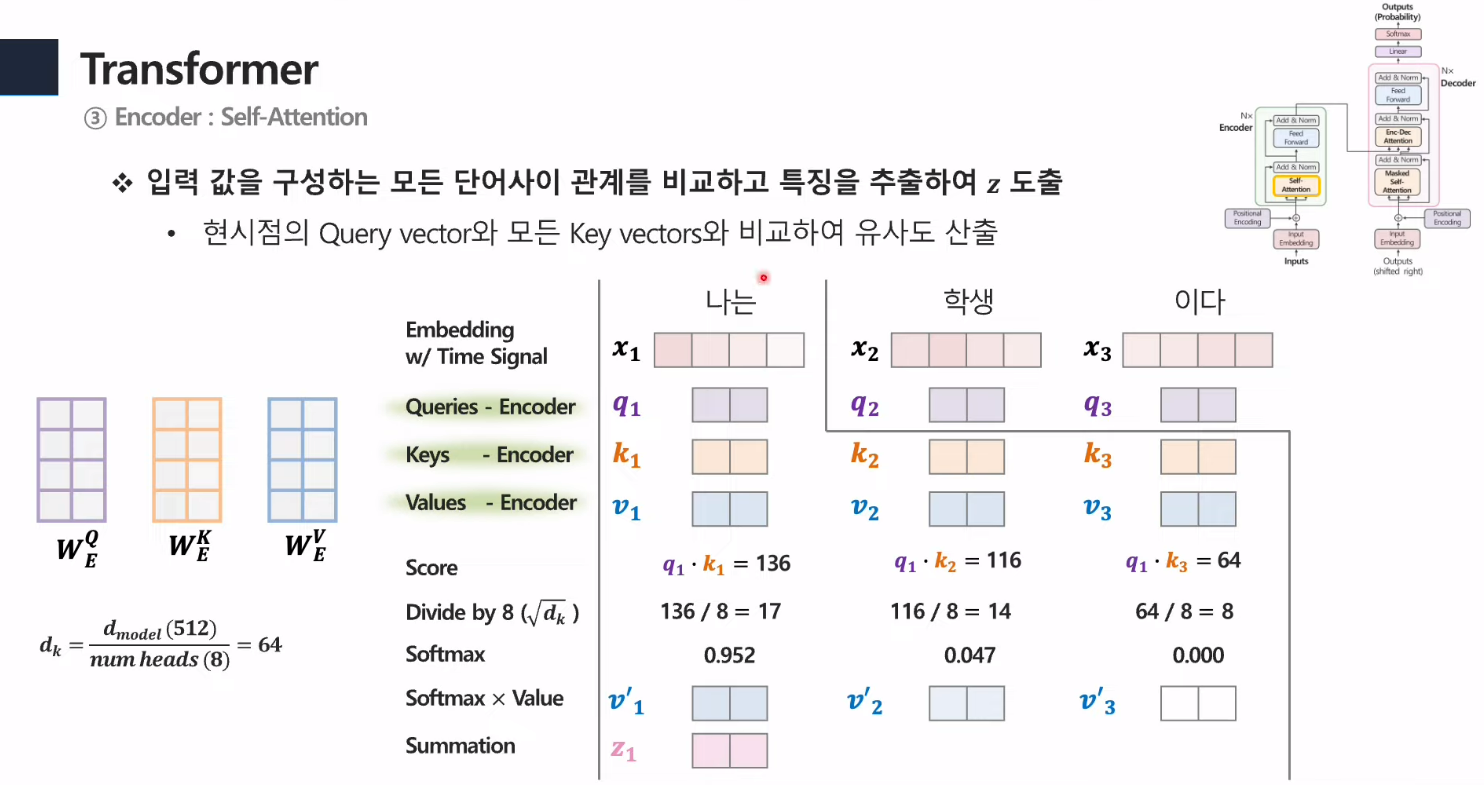
• Q,K,V의 값을 만들고, Q와K끼리의 내적곱을 해줌.

• 이후 scaling 해주고, Softmax 함수에 넣으면 각 단어에 대한 가중치가 만들어짐

• 이 단어의 가중치 값들과 V값을 곱해줌 ⇒ 각 단어에 대한 output(z) 생성.

• 벡터로 내적곱을 표현하면 저렇게 나옴.

• head 개수에 따라 각 해당하는 가중치 개수가 생기게 됨 ⇒ 서로 비슷한 값들의 가중치들이 만들어지기에 결국, 각 head에 해당하는 z 벡터도 값이 다 비슷비슷할거임⇒ 같은 데이터를 쓰지만 다른 가중치를 넣어 다양성 반영을 할 수 있다.(필터와 같은 역할)

• head가 8개이므로 8개의 output이 나오고, 처음 embedding 벡터 크기와 맞춰주기 위해 W0를 곱해줌 ( 그냥 동일한 차원으로 만들어주는 역할로 존재)

3.2 Encoder: Add+Norm

• z(output) 값과 들어가기 전의 embedding에 해당하는 각 벡터를 더해줌.

3-3. Encoder: Feed Forward Network

• 기존 residual network(skip connection)으로 나온 값을 fc layer에 넣음.

• 이때 FC에 대한 파리미터 값은 다 동일함.

• 통과해서 나온 값과 FC 통과 전 값이랑 더해줌.

---

4-1. Decoder: Masked Self-Attention

• 나는 학생이다의 번역본(정답)을 embedding 계층에 넣음.

• positional embedding과 더해줌

• encoder과 마찬가지로, 해당 Q,K,V에 맞는 가중치를 각각 곱해줌.

• I 에 대한 output을 뽑고자 할 때 그 뒤에 있는 단어들은 masked를 거쳐 0으로 만들어줌.

• I에 대한 output 뽑고 두번째 am도 마찬가지

4-2. Decoder: Encoder-Decoder Attention

• am이라고 가정하면 이전 masked 계층에서 나온 I, am의 값을 가져옴. ⇒ Q값이 됨.

• 그다음 encoder에서 가장 마지막에 나온 결과값을 가져옴. I와 am에 관한 정보의 벡터를 K값과 V값으로 씀 (K,V)값은 같음.

• 마찬가지로 multi-head attention 똑같이 해주면 됨.

• Q,K,V 값 가져온걸 각 가중치에 곱해서 head에 맞는 값을 생성 후 Q와 K 내적 곱 후 V와 곱함.

4-3. Decoder: Feed Forward Network

• Add+Norm 해서 각 단어에 대한 값 추출.

5. Prediction

• 각 단어에 대한 값을 softmax 함수에 넣어서 확률로 변환시킴

• 거기서 가장 높은 연관성을 띄는 값을 output으로 내보냄.

6. Model Architecture

+ Positional Encoding는 어떻게 만들어질까? (+추가 궁금증)

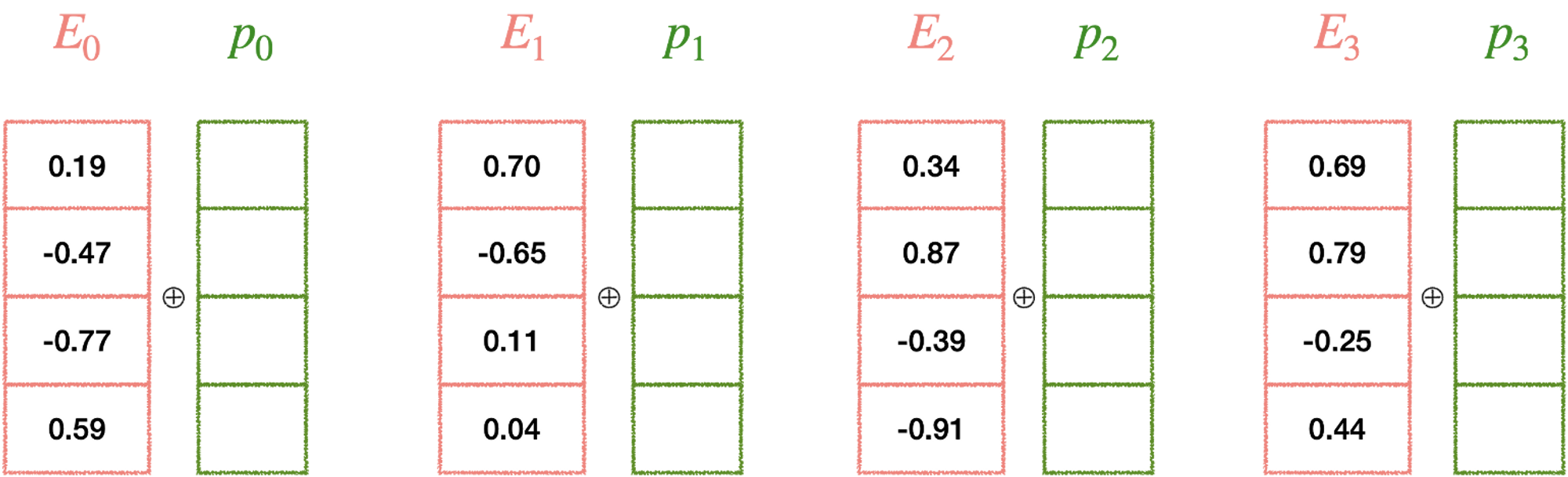
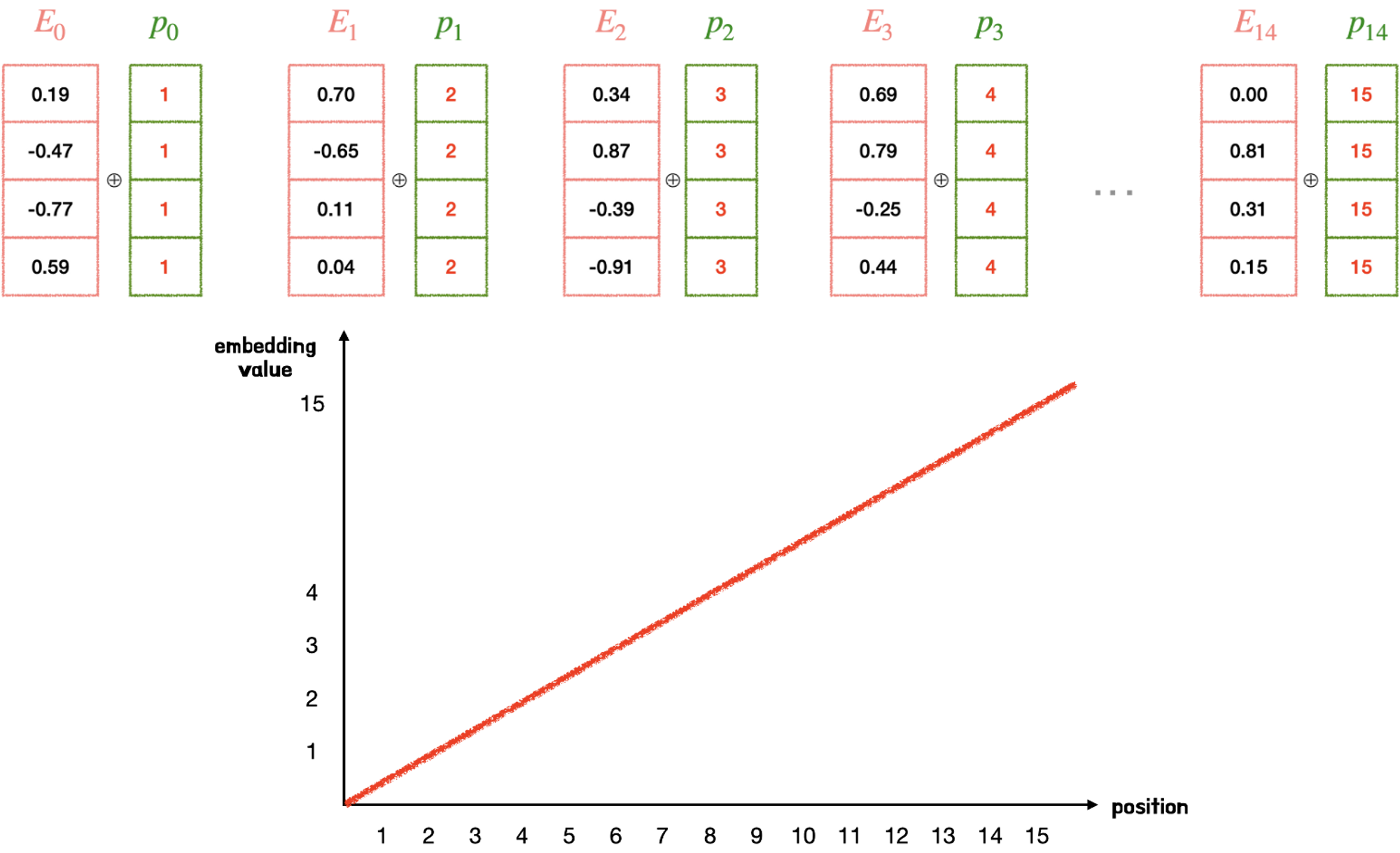
1. positional encoding base

• not의 위치 차이로 인해 두 문장의 뜻이 아예 달라짐→ 문장 내 정확한 단어 위치가 없을 경우, 문장의 뜻이 완전히 달라짐.
• 

• 그렇기 때문에 각 해당하는 단어 벡터에 위치 정보 벡터를 더해야 함.

2. positional encoding의 규칙

• 1. 모든 위치 벡터는 동일하게

  • 모든 위치 벡터는 시퀀스 길이나 Input에 상관없이 동일한 식별자를 가져야 함.

  • 그렇기 때문에 시퀀스가 바껴도 위치 임베딩은 동일하게 유지.

  

• 2. 위치 벡터 값은 너무 크지 않게

  • 위치값이 너무 커지게 되면 단어 간의 상관관계나 의미 정보 값이 작아지게 됨.

  

3. 위치 벡터 생성 방법 및 문제점

• 1. 시퀀스 크기에 비례한 정수값 부과

  • 첫번째 단어의 경우: 1, 두번째 단어: 2 등등으로 부여

  

  • 문장이 길어지면 벡터값 비례해서 엄청나게 증가하게 됨.

  • 특정한 범위를 갖지 않아 일반화 불가

  • 단어 정보에 더하게 될 경우, 위치 정보가 지배적이라 단어 정보가 훼손될 가능성 생성.

• 2. 첫번째 0, 마지막 1, 중간 1/단어수

  

  • 문장 길이에 따라 같은 위치 정보에 해당하는 위치 벡터가 달라지게 됨.

  • 옆에 위치한 벡터 차이도 달라짐.(간격)

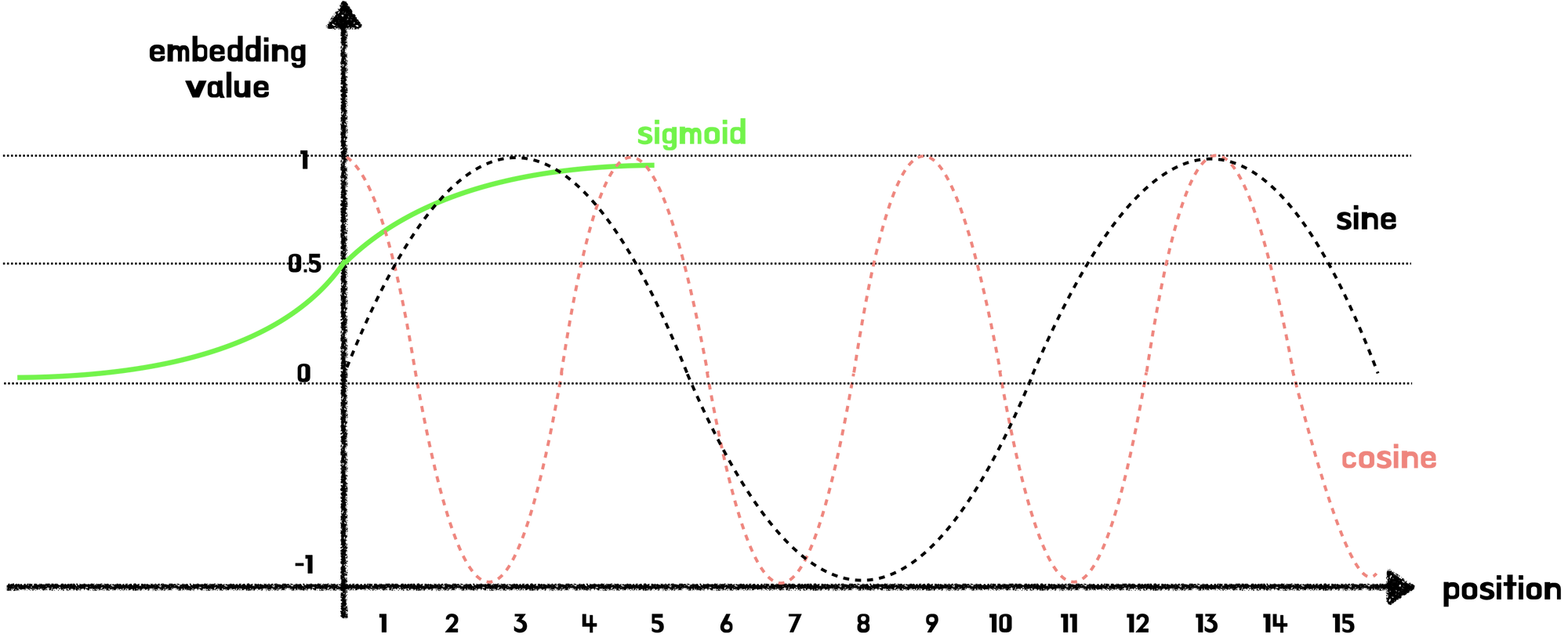
4. Sin&Cos 함수 사용

→ 벡터값이 너무 크면 안되고, 항상 같은 위치의 벡터값을 지녀야 함.

⇒ 그래서 나온 것이 cos&sin 함수

• 1. -1~1의 반복 주기함수

  

  • sigmoid를 쓰면 안되는 이유:⇒ 긴 문장이 오게되면 1에 수렴하게 됨.
  • ⇒ 즉, 위치 벡터값의 차가 미미해짐

  • 그래서 sin과 cos가 적합.

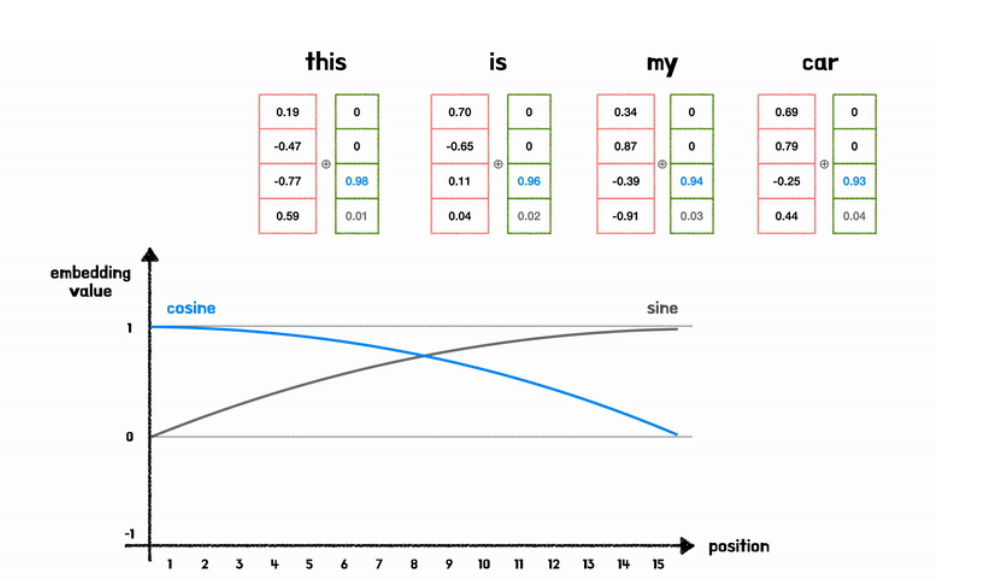
• 2. 항상 같은 위치 벡터 값

  • 한가지 문제점
    • 같은 위치에 있는 단어는 항상 같은 위치 벡터값을 지녀야 함
    • ex) I love you와 I like me 중에서 love와 like의 위치벡터는 같음.

  • 하지만 주기함수이기 때문에 서로 다른 위치의 단어의 경우에도 같은 위치 벡터값이 생성됨. (그림참고)

    

    → postional encoding은 스칼라가 아닌 벡터로 이루어져있어 단어 벡터와 같은 차원을 지님.
  • 

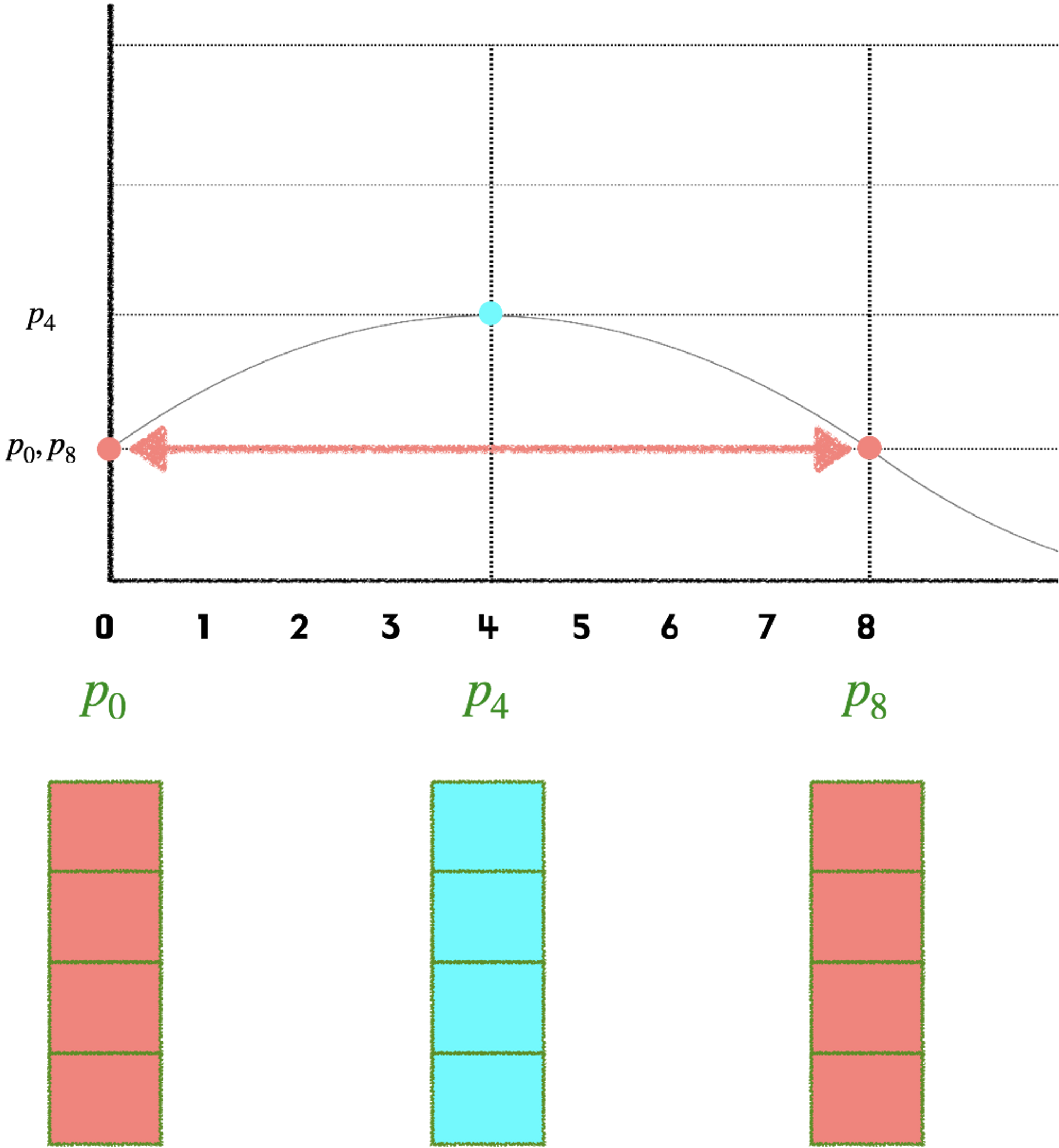
  • 그렇기 때문에 차원이 4개로 표현한다고 가정하면 각 요소는 서로 다른 4개의 주기를 갖게 됨 (짝수 홀수)

  • 따라서 겹치지 않게 됨.

• 2-1) postional encoding vector 값 채워지는 원리

  

  • 첫번째 차원의 벡터 값들의 차이가 크지 않은 경우

  • 벡터 다음 차원에도 벡터값 부여

  

  • 이때 다음 차원에도 sin을 넣으면 벡터들 간의 차가 크지 않기에 cos 활용.

  • 하지만 위의 사진을 보면 벡터값 차이가 크지 않음

  • 이럴 경우, 서로 다른 벡터 간의 위치 정보 차가 미미해짐 (의미 없어짐)

  

  • 이 경우, cos함수의 frequency를 이전 sin함수보다 더 크게 줌.

  

  • sin&cos 반복

  

  • 결론적으로 서로 다른 positional encoding 값을 지니게 됨.

  

5. 왜 concat 안하고 더해줬는가

• concat을 하게 되면 단어 정보 벡터와 위치 정보 벡터 각각 독립된 자체 차원 공간만을 갖게됨. 그렇게 되면 직교 성질에 의해 서로 영향을 줄 수 없게 됨.⇒ 따라서 더해줌으로써 단어 정보와 위치 정보간의 균형을 맞춰줌.

 

 

트랜스포머 transformer positional encoding

트랜스포머 Transformer Attention is All You Need Postional Encoding

https://www.blossominkyung.com/deeplearning/transfomer-positional-encoding